EDSCRATCH 2 - FAHREN NACH FORMEN

DAS PROJEKT

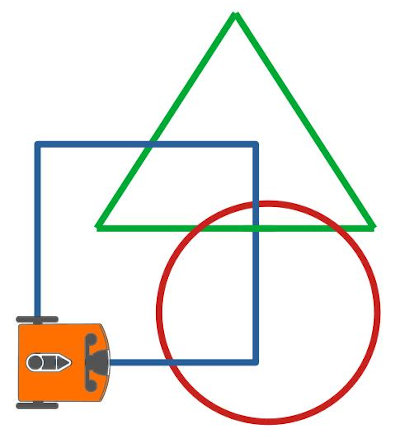
Hast du schon die “Schleifen” kennengelernt, die wir im Projekt “Verkehrsübungsplatz” vorgestellt haben? Falls nicht, solltest du dir das Projekt jetzt anschauen. Hier in diesem Projekt fährst du nämlich die geometrischen Formen Quadrat, Dreieck und Kreis ab. Diese Formen bestehen aus Wiederholungen und bieten sich deshalb für Schleifen an.

Für bessere Ergebnisse beim Fahren geben wir dir zwei Tipps:

Stell die Fahrgeschwindigkeit des Roboters auf langsam.
Verwende das Wait-Kommando. Dieses Kommando hält mit einem Wert von 0.5 Sekunden die Motoren kurz an. Wenn du dieses Kommando zwischen die einzelnen Fahrbefehle setzt, werden die Motoren exakter gesteuert.

Falls du mit Edison auf unserer Vorlage “EdScratch-Formen” fahren möchtest:

Entferne das Gleitstück auf der Unterseite von Edison.
Zum Starten stell Edison mit der gedachten Mitte zwischen seinen Rädern auf eine der Ecken, auf denen er dreht. Die Startposition ist in der Vorlage abgebildet.

Willst du mehr wissen:

Stell dir vor, durch Edison ist von oben nach unten ein Loch gebohrt und darin steckt ein Stift. Mit diesem Stift soll der Roboter während der Fahrt die Form nachzeichnen. An den Ecken von Quadrat und Dreieck soll der Roboter auf der Stelle drehen und der Stift soll dabei an einem Punkt bleiben. Dazu muss der Stift genau dort sein, wo sich die Drehachse für diese Drehung befindet, denn sonst würde der Stift einen Kreisbogen beschreiben.

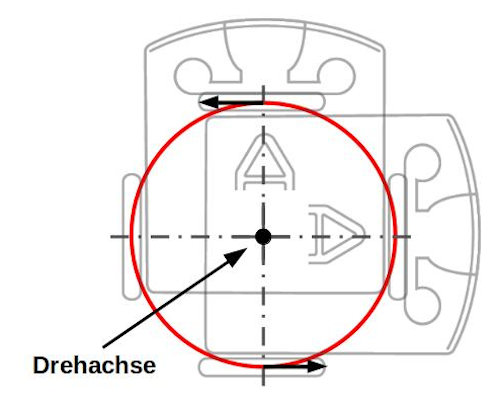
Die Drehachse liegt genau mittig zwischen den beiden Antriebsrädern. Wir verwenden zwar keinen Stift, aber wir richten die Mitte zwischen den Rädern auf eine Ecke von Quadrat/Dreieck aus. So können wir gut verfolgen, ob unsere programmierte Fahrt korrekt ist.

DEINE MISSION

Zuerst wollen wir die Form eines Quadrats nachfahren.
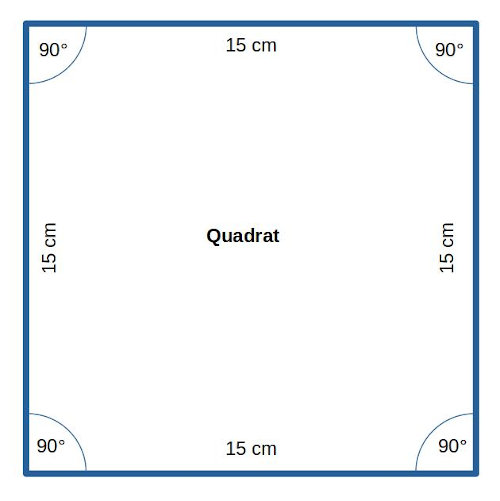
Wissenswertes über Quadrate: ein Quadrat hat vier gleich lange Seiten und vier rechte (90°) Winkel.

Deine Aufgaben:

Schreibe mit EdScratch ein Programm, mit dem der Roboter die Form eines Quadrates abfährt. Die Seitenlänge soll ca. 15 cm betragen. Am Ende soll der Roboter wieder so stehen, wie beim Start. Verwende NUR die Fahrbefehle aus der Kategorie “Drive” (Fahren) und KEINE Schleife!
Wie viele Blöcke benötigst du (der Startblock wird nicht mitgezählt) und was ist dabei auffällig?

Durch Ungenauigkeiten beim Antrieb musst du bei Drehungen vielleicht noch ein paar Grad hinzufügen oder abziehen.

Lösungsvorschlag:

Zuerst haben wir die einzelnen Fahraktionen nacheinander (sequentiell) angeordnet.

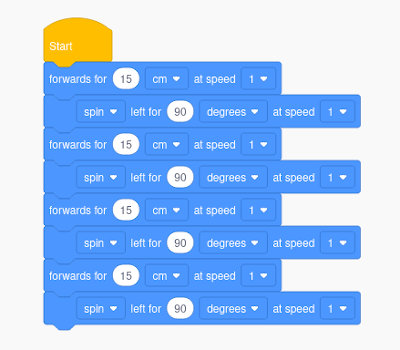
Hinweise zu den Blöcken:

Du benötigst aus Kategorie Drive (Fahren) nur die Befehle “forwards for” (vorwärts für) und “spin” (drehen auf der Stelle). Wir drehen nach links, also “spin left”.
Im Befehl “forwards for” stellen wir die Parameter “15 cm” für die Fahrstrecke und “speed 1” für langsame Geschwindigkeit ein.
Für die Drehung “spin left” stellen wir die Parameter “90 degrees” (90 Grad) und “speed 1” für langsame Geschwindigkeit ein.
Wir benötigen acht Blöcke. Dabei fällt auf, dass viermal die Abfolge “Fahrt vorwärts” und “Drehung links” durchlaufen wird.

Nun programmiere das Quadrat, in dem du eine Schleife verwendest. Wie du eine Schleife verwendest, haben wir im Projekt “Verkehrsübungsplatz” gezeigt.

Deine Aufgaben:

Verändere das Programm, indem du den Block “repeat” (wiederhole) aus Kategorie “Control” (Kontrollstruktur) verwendest.
Wie oft muss die Schleife insgesamt durchlaufen werden?
Wie viele Blöcke (außer Start) benötigst du jetzt?
Setze zum Testen das Wait-Kommando aus Kategorie Control (Kontrollstrukturen) zwischen die einzelnen Fahrbefehle. Fährt der Roboter mit dem Wait-Kommando genauer?

Lösungsvorschlag:

So sieht unser “Quadrat-Programm” mit Schleife aus:

Die Schleife muss viermal durchlaufen werden. Für jede Seite des Quadrats einen Durchlauf.
Wir benötigen statt acht nur noch drei Blöcke. Einen Block für die Schleife und zwei Blöcke für die Fahraktionen.

So sieht unser “Quadrat-Programm” (edscratch_quadrat.ees) mit Schleife und Wait-Kommando aus:

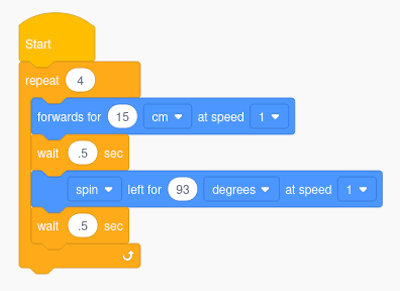
Unser Roboter fährt mit dem Wait-Kommando genauer.

Nun lass uns die Form eines gleichseitigen Dreiecks abfahren.
Wissenswertes über gleichseitige Dreiecke: sie haben drei gleich lange Seiten und drei gleich große Innenwinkel. Da im Dreieck immer alle Innenwinkel zusammen 180° ergeben, ist ein Innenwinkel 180° : 3 = 60°.

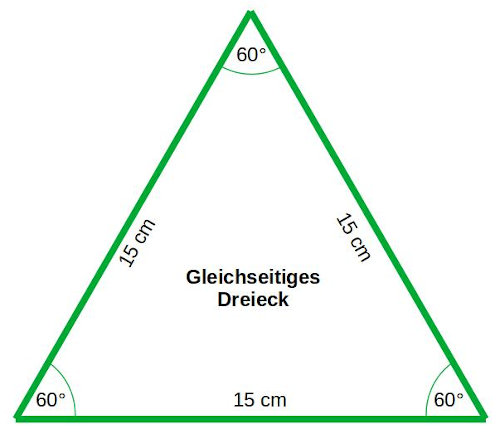
Deine Aufgabe:

Erstelle ein EdScratch-Programm, mit dem der Roboter die Form eines gleichseitigen Dreiecks abfährt. Die Seitenlänge soll ca. 15 cm betragen. Am Ende soll der Roboter wieder so stehen, wie beim Start. Verwende eine Schleife.

Lösungsvorschlag:

Wir sind das Dreieck mit diesem Programm (edison_dreieck.ees) abgefahren:

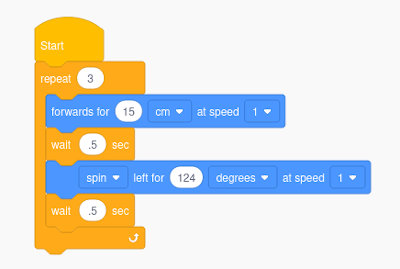
Theoretisch müsste der Winkel für die Drehung 120° betragen. Wegen der Ungenauigkeiten im Antrieb mussten wir bei unserem Roboter 124° angeben, um die Form korrekt abzufahren.
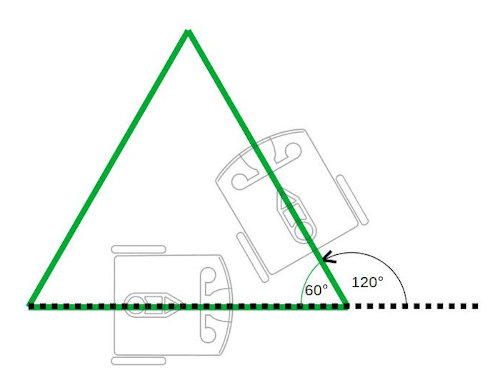
Falls du dich fragst, warum man nicht für die Drehung den Innenwinkel von 60° angeben kann, dann siehe bitte unsere Zeichnung:

Um bei der Fahrt zwischen zwei Geraden einen Innenwinkel von 60° einzuschließen, muss der Roboter aus seiner Fahrtrichtung heraus eine Drehung von 120° machen.

Als Nächstes fahren wir einen Kreis.
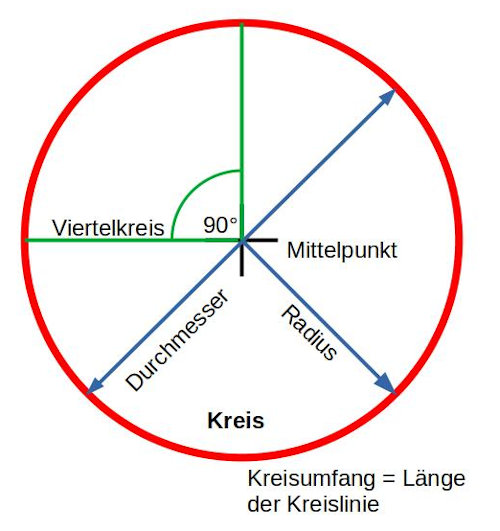
Wissenswertes über Kreise: Alle Punkte auf der Kreislinie haben den gleichen Abstand zum Mittelpunkt. Den Abstand von Kreislinie zum Mittelpunkt nennt man Radius. Der Abstand von Kreislinie zu Kreislinie durch den Mittelpunkt heißt Durchmesser. Die Länge der Kreislinie nennt man Kreisumfang. Der Kreisumfang besteht aus 360 gleichen Abschnitten. Die Winkelweite zwischen den Abschnitten beträgt jeweils 1°. Das bedeutet, ein Viertelkreis entspricht 90°, ein Halbkreis 180° und der Vollkreis 360°.

Unter der Kategorie “Drive” wirst du keinen Befehl finden, bei dem du einen Radius/Durchmesser angibst und der Edison einen entsprechenden Kreis fährt. Vielleicht findest du aber andere Möglichkeiten. Wir werden dir zwei Möglichkeiten zeigen, in einer Kreisform zu fahren.

Deine Aufgabe:

Finde eine einfache Möglichkeit, mit Edison einen Kreis zu fahren. Den Radius kannst du frei wählen.

Lösungsvorschlag:

Das ist unsere Fahrt im Kreis:

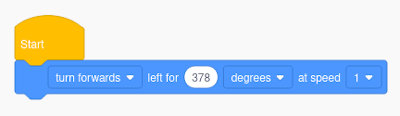
Bei Kurvenfahrten (turn forwards/backwards) dreht das Rad auf der Kurvenaußenseite um das stehende innere Rad – wie bei einem Zirkel.
Theoretisch müsste der Winkel für eine Kurvenfahrt im Vollkreis 360° betragen. Wegen der Ungenauigkeiten im Antrieb mussten wir bei unserem Roboter 378° angeben, um einen vollen Kreis zu fahren.

Zum Abschluss wird es anspruchsvoll! Finde eine Möglichkeit, eine Kreisform mit einem Radius von ca. 8 cm zu fahren.

Tipp: Es gibt keinen EdScratch-Befehl, um einen exakten Kreis mit einem bestimmten Radius zu fahren. Vielleicht kannst du aber eine Kreisform fahren, wenn du viele Geraden aneinander reihst.

Deine Aufgabe:

Erstelle mit Ed-Sratch ein Programm, mit dem Edison eine Kreisform fährt. Der Radius soll ca. 8 cm betragen.
Einen Lösungsansatz siehst du auf unserer Vorlage “EdScratch – Formen” bei Kreis 2.
Was fällt dir auf, wenn du dir alle Lösungen anschaust? Den “einfachen Kreis” mit der Kurvenfahrt lassen wir dabei außen vor.

Lösungsvorschlag:

So machen wir unsere Kreisfahrt (edison_kreis.ees):

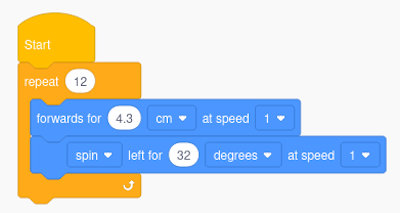
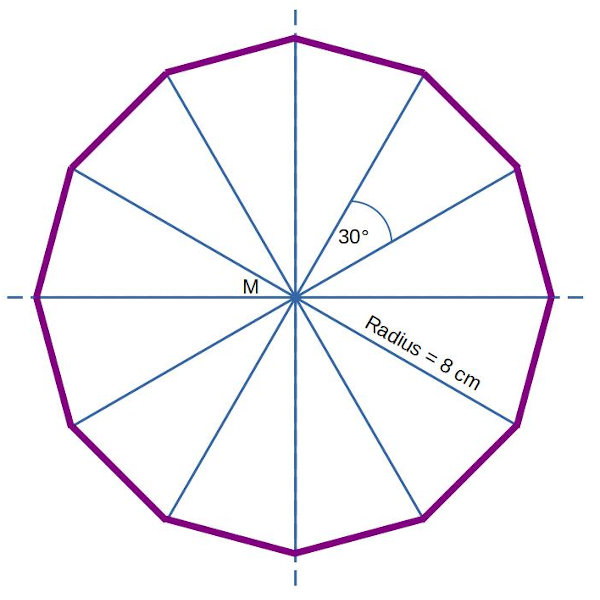
Wir haben den Kreis in ein Zwölfeck zerlegt. Die Fahrt wird umso kreisförmiger, je mehr Ecken du festlegst.

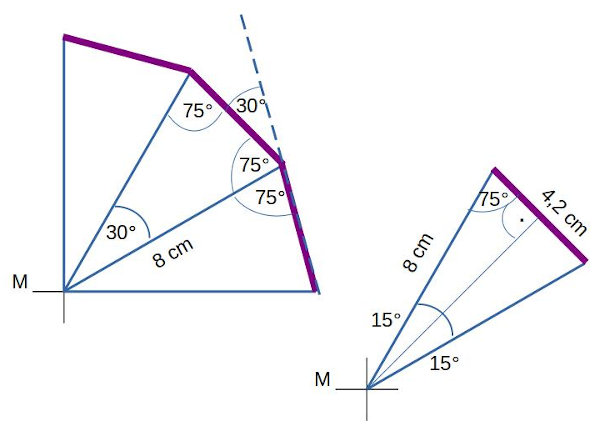
Die Seitenlänge des Zwölfecks und den Winkel, um den Edison drehen soll, kannst du entweder aus unserer Zeichnung entnehmen oder besser errechnen.

Wir zerlegen das Zwölfeck in 12 Dreiecke. Jedes Dreieck hat eine Schenkellänge von 8cm und ist gleichschenklig. Die Winkel an den Schenkeln sind (180° – 30°) : 2 = 75°
Edison dreht um 30° (180° – 2 * 75°) aus seiner Fahrtrichtung.
Die zu fahrende Seitenlänge erhalten wir mittels sinus α = Gegenkathete : Hypothenuse.
Gegenkathete = sinus α * Hypothenuse = sinus 15° * 8 cm ≈ 2,1 cm.
Seitenlänge = 2 * Gegenkathete = 2 * 2,1 cm = 4,2 cm.
Rechnerisch sollte Edison 4,2cm vorwärts fahren und um 30° auf der Stelle drehen. Wegen der Ungenauigkeiten im Antrieb haben wir die Parameter etwas angepasst.
Da es sich um ein Zwölfeck handelt, führt das Programm die Aktionen Vorwärtsfahrt und Drehung zwölfmal hintereinander aus.
Bei den geometrischen Figuren Quadrat, Dreieck und einem Vieleck (Zwölfeck) sieht die Lösung immer gleich aus. Einer Vorwärtsfahrt schließt sich eine Drehung an. Das wird sooft wiederholt, wie die Figur Ecken/Seiten hat. Wir haben einen sogenannten Algorithmus gefunden, mit dem regelmäßige Polygone/Vielecke abgefahren werden können. Ein Algorithmus ist eine Lösungsanweisung für eine bestimmte Aufgabe.

Falls du Spaß an der Kombination aus Geometrie und Programmierung hast, solltest du dir die Webseiten “Turtle Academy” und “TurtleCoder” anschauen.

Was du bei diesem Projekt lernen kannst:

Geometrie ist ein mathematisches Werkzeug, mit dem wir Fahraufgaben lösen können.
EdScratch bietet verschiedene Möglichkeiten um Kurven zu fahren. In einem EdScratch-Block kannst du festlegen, ob der Roboter auf der Stelle drehen (spin) soll, ob er eine Kurve nach vorn (turn forwards) oder nach hinten (turn backwards) fahren soll. Bei Kurvenfahrten mit turn dreht das Rad auf der Kurvenaußenseite um das stehende innere Rad.
Einige geometrische Formen bestehen nur aus Wiederholungen. Für Wiederholungen setzen Programmierer “Schleifen” ein.
Wir haben “nebenbei” einen Algorithmus für das Abfahren von regelmäßigen Vielecken gefunden. Ein Algorithmus ist eine Lösungsanweisung für eine bestimmte Aufgaben. In unserem Fall sieht der Algorithmus so aus:
1.) Fahre eine bestimmte Länge vorwärts.
2.) Drehe um einen bestimmten Winkel auf der Stelle.
3.) Wiederhole Vorwärtsfahrt und Drehung sooft, wie die Figur Ecken/Seiten hat.
Edison ist ein günstiger Roboter und kein teures Präzisionsgerät. Deshalb kann es zu kleinen Abweichungen beim Fahren kommen. Das können wir beim Drehen durch Anpassen der Winkel berücksichtigen.